Is it really possible to achieve incoherent beam combining with optimal output quality?

In Star Wars, the Death Star was George Lucas’ idea of how several lasers could be combined to form a single, more powerful output beam. In this article, we invite you to discover Cailabs’ innovative method of incoherent beam combining…
In a previous blog post, David Allioux talked about using incoherent beam combining to overcome the power limitation of lasers without having to control their respective phases. In the near future, we hope to be able to quickly heat David’s pumpkin soup to a satisfactory temperature, and most importantly to use these combiners for various other infrared photonic applications, such as LiDARs, countermeasure and spectrometry.
However, a trade-off is necessary, and it is impossible to combine several multimode lasers efficiently without increasing divergence (i.e. affecting the output beam quality).
Two factors are generally used to quantify the performance of laser combining techniques: combining efficiency, i.e. the fraction of power of the combined beam relative to the total summed power of the N combined sources, and beam quality factor, denoted by M². In this article, we will focus specifically on this last key factor.
M² is a term from physics that describes the difference between a beam’s divergence angle and an ideal Gaussian beam. A lower value corresponds to a higher quality focus. In other words, the closer the value is to 1, the more the beam will qualify as “single-mode” and the closer it is to a perfect Gaussian beam.
1- Cailabs’ solution: Manipulating light modes
To begin with, and at the risk of disappointing fans of Emperor Palpatine, we must point out that the method is quite different than that of the Death Star illustrated below…

By “combining” eight converging beams, each beam of the star would cross each other and continue to propagate in its own direction. It is therefore imperative that all input beams are collinear and merged at output.
To optimally combine several sources, Cailabs proposes a modal approach consisting of decomposing any form of light on the basis of arbitrary spatial modes. There are several conventional bases, such as the Hermite-Gauss or Laguerre-Gauss modes, which are commonly used in optics.
Light is an electromagnetic wave which, when propagated in a homogeneous medium, is subject to Maxwell’s equations. Any wave propagating in an isotropic medium (medium with the same physical properties in all directions) must satisfy the propagation equation. The spatial modes represent the solutions to this light propagation equation.
These modes therefore retain the same profile as they propagate. They may expand or fluctuate in the presence of atmospheric turbulence, but overall, the modes are preserved. Spatial modes such as Hermite-Gaussian or Laguerre-Gaussian form a spatial basis. They can be conveniently used to describe any spatial profile of a light beam.
2- What is the ideal combiner?
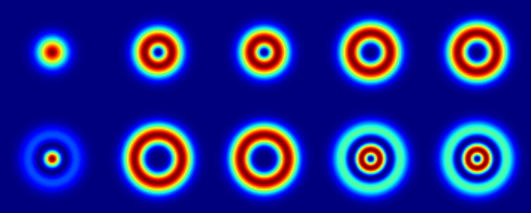
For a multimode beam composed of N LG modes (see figure 2) of equal power and incoherent between each other, the M² factor can be written as the average of the summed LG modes(1):
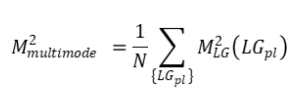
This last equation enables us numerically to obtain the properties of an optimal combiner since we can show that it is the superposition of Laguerre-Gauss modes which has the lowest M² factor.
The expression M2multimode gives the following table:

It is thus theoretically possible to combine 10 incoherent single-mode beams of the same power into a multimode beam with an M²=3.
The intensity profile of the sum of the 10 LG modes is shown in the diagram below:
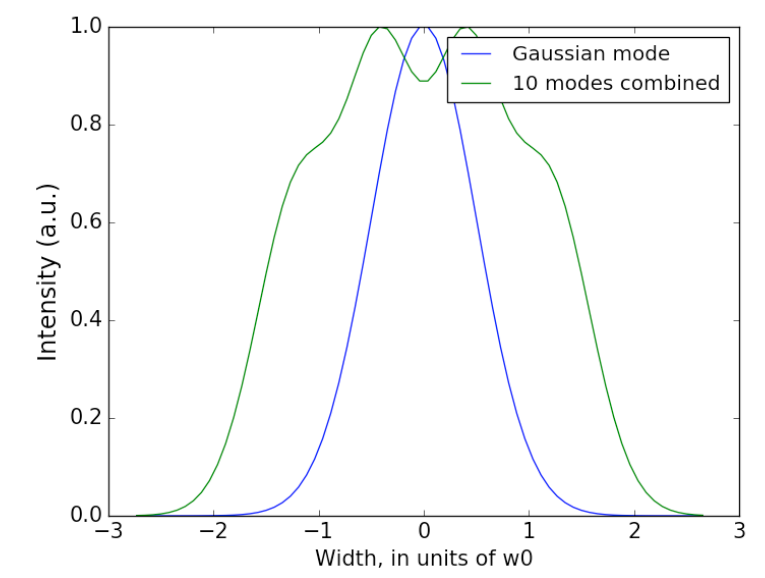
The incoherent sum of the LG modes therefore makes it possible to increase the power with minimal deterioration of the M² factor.
By converting each input source into a given LG mode and combining (summing) each converted input, an optimal combined output beam is obtained.
3- How can this optimal combined beam be obtained?
In other words, is there a device that can convert each input into a given spatial mode while ensuring controlled losses in order to achieve good combining efficiency?
The strength of Cailabs’ MPLC (Multi-Plane Light Conversion) technology lies in its ability to convert, manipulate and decompose any beam into modes in a given basis.
MPLC makes it possible to transform a given number of single-mode lasers into the same number of lower order Laguerre-Gauss modes. The device therefore enables optimal combining of incoherent sources and minimizes divergence of the combined beam.
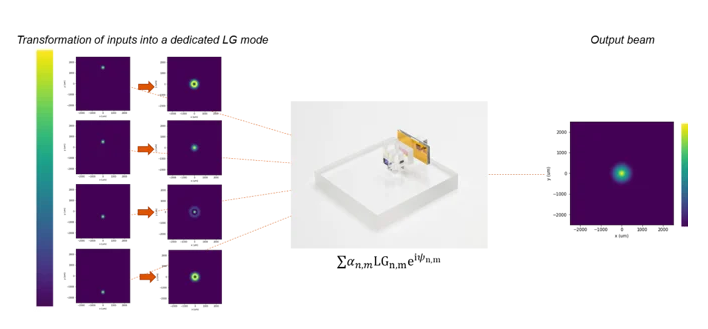
4- That seems like a great idea on paper, but will it work in practice?
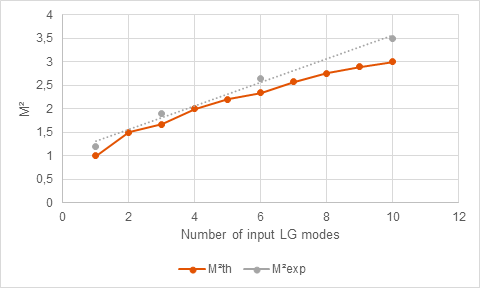
Once the tool was identified, the theory still had to be validated through experiments.

Cailabs did just that in 2017, achieving performances very close to the values of M2theorical set out above.
5- Outlook

Since 2017, Cailabs has been working to further improve these results and offer ever more powerful and efficient combiners.
As a result, MPLC is today a key essential technology which in the very near future will be able to combine incoherent sources while producing a good quality output beam.
Mid-infrared (MIR) optronic systems, such as countermeasure applications require high power sources in the 4 to 5 µm range, however the power of current sources is limited. Cailabs’ incoherent combiners will allow you to bridge this gap… and heat your soup faster.
Sources :
(1) Fast adaptive laser shaping based on multiple laser incoherent combining – L. Garcia, O. Pinel, P. Jian, N. Barré, L. Jaffrès, J.-F. Morizur, G. Labroille – SPIE Photonics West LASE, 10097-3 (2017) - Read the abstract
Annex : ISO 11146-1:2004 Standard:
The M² is computed as the average of the M²x and M²y measured on the two axes orthogonal to the propagation axis.

Par Tangi Le Guennic
Tangi Le Guennic, who holds Master’s degrees in materials science and optics, is a project and product manager at Cailabs. Tangi has a strong experience in R&D in developing optical sensors for aircraft systems as well as in industrial vision project management. At Cailabs, he works on the development and commercialization of innovative optical solutions for PROTEUS and custom applications (defense, aeronautics, automotive, biomedical…).
